Question

If he(g) has an average kinetic energy of 8750 j/mol under certain conditions, what is the root mean square speed of cl2(g) molecules under the same conditions?

Answer 1

The root mean square speed is given by V_rms = âšRT/M where r, t, and m are the rate constant, temperature and molar mass the gas Average molar kinetic energy of the gas E = 1/2 M * (V_rms)^2 = 8750 ms/1 So (V_rms)^2 = (2 * 8750) / M Molar mass of 2 chlorine atoms in kg is 2 * 35 * 10^(-3) Hence we have (V_rms)^2 = (2 * 8750)/ (2 * 35 * 10^(-3)) (V_rms)^2 = 8750/0.035 = 250000 So V_rms = âš 250000 = 500

Answer 2

18.74 m/s is the root mean square speed of chlorine gas molecules under the same conditions.

Step-by-step explanation:

Average kinetic energy is defined as the average of the kinetic energies of all the particles present in a system. It is determined by the equation:

`K.E=(3RT)/(2)`

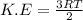
where,

K.E = Average kinetic energy

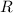`R` =Universal gas constant =8.314 J /mol K

T = Temperature of the system

He has an average kinetic energy of 8750 J/mol

`8750 J/mol =(3* 8.314 J/mol K* T)/(2)`

T =
`(8750 J/mol * 2)/(3* 8.314 J/mol K)`

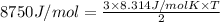
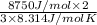
T = 701.63 K

The formula used for root mean square speed is:

`\\u_(rms)=\sqrt{(3kN_AT)/(M)}`

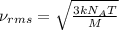
where,

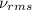`\\u_(rms)` = root mean square speed

k = Boltzmann’s constant =
`1.38* 10^(-23)J/K`

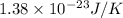
T = temperature =701.63 K

M = atomic mass = 0.071 kg/mole

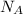`N_A` = Avogadro’s number =
`6.02* 10^(23)mol^(-1)`

`\\u_(rms)=\sqrt{(3* 1.38* 10^(-23)J/K* 6.022* 10^(23) mol^(-1)* 701.63 K)/(0.071 kg/mol)}`

`\\u_(rms)=18.74 m/s`

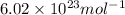
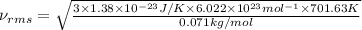
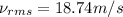
18.74 m/s is the root mean square speed of chlorine gas molecules under the same conditions.