Question

A cola-dispensing machine is set to dispense a mean of 2.02 liters into a container labeled 2 liters. actual quantities dispensed vary and the amounts are normally distributed with a standard deviation of 0.015 liters. what is the probability a container will have less than 2 liters?

Answer 1

Answer: 0.9087.

Explanation:

Given : Population mean :
`\mu=2.02\text{ liters}`

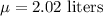
Standard deviation :
`\sigma =0.015\text{ liters}`

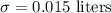
Here , the actual quantities dispensed vary and the amounts are normally distributed .

Let x be the amount of cola in container in liters :-

`P(x<2)=P((x-\mu)/(\sigam)<(2-2.02)/(0.015))\\\\=P(z<-1.33333)\ \ \ [\because\ z=(x-\mu)/(\sigma)}]\\\\= 0.9087\ \ [\text{Using P-value table}]`

Thus , the probability a container will have less than 2 liters is 0.9087.