Question

Use the following graph of the function f(x) = 3x4 − x3 + 3x2 + x − 3 to answer this question: graph of 3 x to the fourth, minus x cubed, plus 3 x squared, plus x minus 3 What is the average rate of change from x = 0 to x = 1

Answer 1

f(x) = 3x^4 - x³ + 3x² + x - 3
x = 0f(0) = 3(0)^4 - 0³ + 3(0²) + 0 - 3f(0) = 0 - 0 + 0 + 0 - 3f(0) = -3
f(1) = 3(1)^4 - 1³ + 3(1²) + 1 - 3f(1) = 3 - 1 + 3 + 1 -3f(1) = 7 - 4f(1) = 3
x = 0 : f(0) = -3x = 1 ; f(1) = 3
1 - 0 / 3 - (-3) = 1 / 6

Answer 2

the average rate of change = 6

Explanation:

`f(x) = 3x^4 - x^3 + 3x^2 + x - 3`

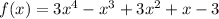
To find average rate of change from x=0 to x=1 we apply formula

`Average = (f(b)-f(a))/(b-a)`

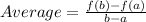
here a= 0 and b = 1

Lets find out f(b) that is f(1), plug in 1 for x in f(x)

`f(1) = 3(1)^4 - (1)^3 + 3(1)^2 + (1) - 3=3`

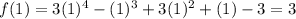
Plug in 0 for x

`f(0) = 3(0)^4 - (0)^3 + 3(0)^2 + (0) - 3=-3`

f(0)= -3, f(1)=3, a=0, b=1. Now apply formula

`Average = (f(1)-f(0))/(1-0)`

`Average = (3-(-3))/(1)=6`

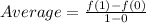
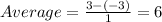
the average rate of change from x = 0 to x = 1 is 6