Answer:
The length of segment RS is:
2.4 units.
Explanation:
We will use the Law of Cosine to find the length of segment RS.
Let the segment RS be denoted by 'c'.
Let a=RQ=2.4 units.
b=QS=3.1 units.
Now, according to the law of cosine we have:

On equating the first two equalities we have:
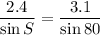
Hence, on solving we get:
S=49.68°
Now as we know that in a triangle the sum of all the angles of a triangle is:
180 degree.
Hence,
∠Q+∠R+∠S=180°
⇒ ∠Q+80°+49.68°=180°
⇒ ∠Q=50.32°
Similarly, on equating the second and third equality we have:

Hence, the length of line segment is:
2.4 units.