Question

What is the approximate measure of angle K? Use the law of sines to find the answer.

20°
34°
41°
53°

Answer 1

34 should be the answer

Answer 2

B. 34°

Explanation:

We have been given an image of a triangle and we are asked to find the measure of angle K.

We will use law of sines to solve our given problem.

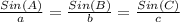`(Sin(A))/(a)=(Sin(B))/(b)=(Sin(C))/(c)`, where, a, b and c are sides corresponding to angle A, angle B and angle C respectively.

Upon substituting our given values in above formula we will get,

`(Sin(K))/(2.7)=(Sin(105^(\circ)))/(4.7)`

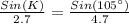
Upon multiplying both sides of our equation by 2.7 we will get,

`(Sin(K))/(2.7)* 2.7=(Sin(105^(\circ)))/(4.7)* 2.7`

`Sin(K)=(0.965925826289)/(4.7)* 2.7`

`Sin(K)=0.2055161332529787* 2.7`

`Sin(K)=0.55489355978304249`

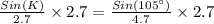
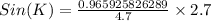
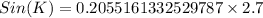
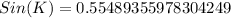
Now we will use arcsin to find the measure of angle K.

`K=Sin^(-1)(0.55489355978304249)`

`K=33.703383757351^(\circ)`

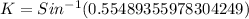
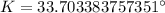
Upon rounding our answer to nearest whole number we will get,

`K\approx 34^(\circ)`

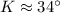
Therefore, the measure of angle K is approximately 34 degrees and option B is the correct choice.