Question

The product of two consecutive integers is 1 more than their sum. find the integers

Answer 1

Let x = the 1st integer , then let x + 1 = the next integer

We can then write the following equation:

x(x+1) = [x + (x+1)] +1 and simplifying both sides gives

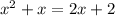
`x^(2) + x = 2x + 2` Collecting all terms on the left side we have:

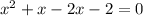
`x^(2) +x-2x-2=0` simplify again

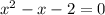
`x^(2) -x-2=0` We can now solve by factoring:
(x - 2)(x + 1) = 0 or x = 2 and x = -1

Now if "X" can be 2 or -1 that means there are 2 possible sets of consecutive integers: 2,3 and -1,0

If you check, both of these satisfy our original conditions of the consecutive integers. Product = Sum + 1