Question

What are the discontinuities of the function f(x) = the quantity x squared minus 16 over the quantity 4x plus 24?

x ≠ − 4
x ≠ 4
x ≠ − 6
x ≠ 6

Answer 1

Answer with Step-by-step explanation:

we are given a function:

`f(x)=(x^2-16)/(4x+24)`

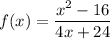
We have to find the point of discontinuity of the function.

As we can clearly see that the function is not well defined if the denominator is zero.

So, the point of discontinuity is that value of x where denominator is zero

i.e. x such that 4x+24=0

4x= -24

x= -6

Hence, function is discontinuous at x= -6

and is continuous at all x ≠ -6

Answer 2

The first thing we should do is write the function:
(x ^ 2-16) / (4x + 24)
This function represents a discontinuity in the x that make the denominator zero.
We have then
4x + 24 = 0
x = -24 / 4 = -6
answer
the discontinuities of the function f (x) is x ≠ - 6