Question

Derivatives (6x)(e^5x)

Answer 1

`\displaystyle (dy)/(dx) = 6e^\big{5x}(5x + 1)`

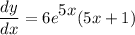
General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Derivative Rule [Product Rule]:
`\displaystyle (d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)`

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Explanation:

Step 1: Define

Identify

`\displaystyle y = 6xe^\big{5x}`

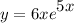
Step 2: Differentiate

1. Derivative Rule [Product Rule]:
   `\displaystyle y' = (d)/(dx)[6x]e^\big{5x} + 6x(d)/(dx)[e^\big{5x}]`
2. Rewrite [Derivative Property - Multiplied Constant]:
   `\displaystyle y' = 6(d)/(dx)[x]e^\big{5x} + 6x(d)/(dx)[e^\big{5x}]`
3. Basic Power Rule:
   `\displaystyle y' = 6e^\big{5x} + 6x(d)/(dx)[e^\big{5x}]`
4. Exponential Differentiation [Derivative Rule - Chain Rule]:
   `\displaystyle y' = 6e^\big{5x} + 6xe^\big{5x}(d)/(dx)[5x]`
5. Rewrite [Derivative Property - Multiplied Constant]:
   `\displaystyle y' = 6e^\big{5x} + 30xe^\big{5x}(d)/(dx)[x]`
6. Basic Power Rule:
   `\displaystyle y' = 6e^\big{5x} + 30xe^\big{5x}`
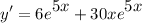
7. Factor:
   `\displaystyle y' = 6e^\big{5x}(5x + 1)`

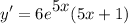
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Differentiation