Question

What is the area of this figure? Enter your answer in the box. in² A parallelogram with a right triangle created inside it with a short leg length of 16 inches and a long leg length of 20 inches. A triangle attached to the top of the parallelogram has a short leg measurement of 8 inches.

Answer 1

I constructed the figure with the information that you provide, please check the picture.
Since there is a right triangle inside the parallelogram, the parallelogram is a rectangle with
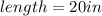
`length=20in` and
`width=16in`; remember that the area of a rectangle is (length)(width), so we can substitute our values to find its area:

`A=(20in)(16in)`

`A=320in^(2)`
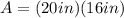
On the other hand, the triangle attached to the top of the parallelogram has
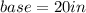
`base=20in`, and
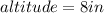
`altitude=8in`; since the area of a triangle is
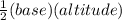
`(1)/(2) (base)(altitude)`, we can substitute our values to get:

`A= (1)/(2) (20in)(8in)`

`A=80in^(2)`

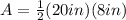
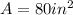
Now the only thing lefts is add the area of the parallelogram and the triangle to get our total area:

`totalA=320in^(2) +80in^(2) =400in x^(2)`

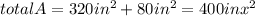
We can conclude that the area of the figure is
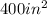
`400in^(2)`.