Question

How many ways can one re-arrange the letters in the word quibble to form a string of 7 letter strings or words, sensible or not?

Answer 1

If the two
`b`s are considered distinct, then the number of such words is


`7!=5040`

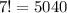
If the two
`b`s are indistinct,


`(7!)/(2!)=\frac{5040}2=2520`

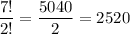
To clarify, "quibble" has 7 possible character positions, and as we draw 1 letter from the pool
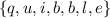
`\{q, u, i, b, b, l, e\}`, we have 1 less letter to choose from for the next character position. So there are


`7*6*5*4*3*2*1=7!=5040`

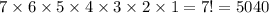
possible words.

If, however, we consider the two
`b`s to be indistinct, so that, for example,
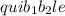
`quib_1b_2le` and
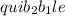
`quib_2b_1le` both count as the same word, then we have to divide the previous total by the number of ways we can rearrange the
`b`s, which is
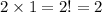
`2*1=2!=2`.