Answer:
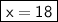
Explanation:
To find the value of x, you have to use the supplementary angles which is equal to 180°.
Supplementary angles = 180°
5x-11+6x-7=180
Combine like terms.
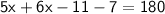
5x+6x=11x

Subtract the numbers from left to right.
-11-7=-18
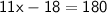
You have to add by 18 from both sides.
11x-18+18=180+18
Solve.
Add the numbers from left to right.
180+18=198
11x=198
Divide by 11 from both sides.
11x/11=198/11
Solve.
198/11=18
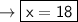
Therefore, the final answer is x=18.