Answer: Volume of vanilla ice cream in the cone=

Explanation:
Given : The diameter of cone = : d= 2 inches
Then radius of cone = Half of diameter = 1 inch
Height of cone = 6 inches.
Volume of cone =
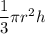 , where r= radius , h= height of cone.
, where r= radius , h= height of cone.
Then, Volume of cone =
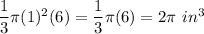
Since ice cream cone is filled with a vanilla and chocolate ice cream at a ratio of 2:
1.
Let x be the volume of chocolate ice cream , then the volume of vanilla ice-cream will be 2x.
Also, Volume of cone=Volume of vanilla ice cream + Volume of chocolate ice cream
i.e.
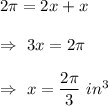
Then , the volume of vanilla ice cream in the cone=
