Solve this equation : (3^7)/(3^x)=3^2^2 Please show all of your work, thanks! :)

Question

Solve this equation :


`(3^7)/(3^x)=3^2^2`

Please show all of your work, thanks! :)

Answer 1

You need to know some basic rules about exponents before you can attempt to solve your question.

`a^b * a^c = a^(b+c)`

`(a^b)/(a^c) = a^(b-c)`

`(a^b)^c = a^((b* c))`

`a^b = a^c \Rightarrow b = c`

Knowing that, you'll see that your question is actually pretty simple.

`(3^7)/(3^x) =3^(22) \\ \\ 3^(7-x) = 3^(22) \\ \\ 7 - x = 22\\ \\ 7 = 22 + x \\ \\ x = 7 - 22 = \boxed{\bf{-15}}`

x = -15

Answer 2

Hey there!

To start, when you have exponents with the same base, you can combine the powers. In the case of
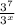
`(3^7)/(3^x)`, you can combine the two exponents by subtracting the powers from one another while keeping the base the same since you have a fraction.

This should result in this new equation:

`3^(7-x)`=
`3^(22)`

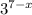
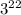
Because the bases of the two numbers are the same, you can set up this expression to solve for the value of x:
7-x=22
-x=15
x=-15

Therefore, your final answer would be x=-15.

Hope this helps and have a marvelous day!