Answer:
The answer is C. 6.2
Explanation:
In order to determine the "x" value, we have to know about right triangles.
A right triangle is triangle with an angle of 90 degrees (pi/2 radians). The sides a, b, and c of such a triangle satisfy the Pythagorean theorem .

where the largest side is conventionally denoted c and is called the hypotenuse. The other two sides of lengths a and b are called legs, or sometimes catheti.
Also, there are some relations called "trigonometric relations". These formulas relation the angles and sides of a right triangle.
I have attached an image that shows the trigonometric relations in a right triangle.
According to the image,
Angle=20 degrees
Opposite side= X
Hypotenuse= 18
We use the "sine" trigonometric relation:
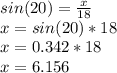
The rounded result to the nearest tenth is 6.2, so the answer is C.