Question

The curved part of this figures is a semicircle.

What is the best approximation for the area of this figure?


28+16.25π units²

14+16.25π units²

14+8.125π units²

28+8.125π units²

Answer 1

The answer is 14 + 8.125 units. 

Answer 2

First we join the two endpoints of the semicircle and that will be the diameter.

And to find the length of the diameter, we have to use distance formula, with one endpoint (3,2) and the other is (-4,-2) .

SO we get

`Diameter = \sqrt{ {-4-3)^2 +(-2-2)^2 } = √(49+16) = \sqrt 65`

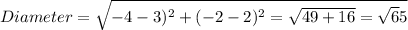
Radius is half of diameter, so the radius is

`Radius= ( √(65))/(2)`

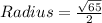
Formula of area of circle is

`Area = \pi r^2`

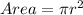
So the area of semicircle is

`=(1/2) \pi ( ( √(65))/(2))^2 = 8.125 \pi \square \units`

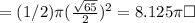
And the other figure is a triangle, with

`image`

`Area = (1/2)*4*7= 14 square units`

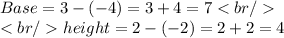
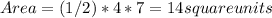
Therefore, total area is the sum of area of semicircle and area of triangle,

And we will get

`Total \ area= 14 + 8.125 \pi \ units^2`

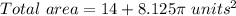
Correct option is the third option .