Question

In the figure, two parallel lines are cut by a transversal. The measure of

angle 1 is 118°. What is the measure of angle 4?

Answer 1

Answer: It would have to be something that adds up to 180.

Explanation:

like if angle 1 is 118 you would add (x) to get to 180.

Answer 2

The measure of angle 4 is also 118° because it is an alternate interior angle to angle 1 with respect to the two parallel lines and the transversal.

The figure in question features two parallel lines cut by a transversal, which creates several angles. When a pair of parallel lines are cut by a transversal, several angle relationships are formed. One of these is that alternate interior angles are congruent.

Here are the steps to find the measure of angle 4 given that the measure of angle 1 is 118°:

1. Identify the relationship between angle 1 and angle 4: If the lines are parallel and angle 1 is an alternate interior angle to angle 4, then they are equal because alternate interior angles are congruent for parallel lines cut by a transversal.

2. State the relationship: Since angle 1 and angle 4 are alternate interior angles, we have:

`\[ \angle 1 = \angle 4 \]`

3. Apply the given information: Angle 1 is given as 118°, so:

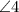`\[ \angle 4` = 118°