Question

Mark and ann together were allocated n boxes of cookies to sell for a club project. mark sold 10 boxes less than n and ann sold 2 boxes less than n. if mark and ann have each sold at least one box of cookies, but together they have sold less than n boxes, what is the value of n ?

Answer 1

`n=11`

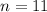
Step-by-step explanation:

Let m represent the number of boxes sold by mark and a represent the number of boxes sold by Ann.

We have been given that Mark sold 10 boxes less than n. We can represent this information in an equation as:

`m=n-10...(1)`

We are also told that Ann sold 2 boxes less than n. We can represent this information in an equation as:

`a=n-2...(1)`

Further, we are told that together they have sold less than n boxes. We can represent this information in an inequality as:

`a+m<n...(3)`

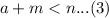
Now we will use substitution method to solve our system of equations.

Upon substituting equation (1) and (2) in (3) we will get,

`n-2+n-10<n`

`2n-12<n`

`2n<n+12`

`2n-12+12<n+12`

`2n-n<n-n+12`

`n<12`

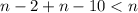
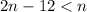
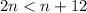
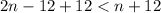
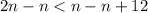
The integer less than 12 is 11, therefore, the value of n is 11.

Answer 2

n = 11.

Step-by-step explanation:
Let m be the number of boxes Mark sells and a be the number of boxes Ann sells.

Since Mark sells 10 less than n, m = n-10. Since Ann sells 2 less than n, a = n-2.

Together, they sold n-10+n-2=2n-12 boxes.

We know that they sold less than n boxes, so our inequality would be
2n-12<n.

To solve this, subtract n from both sides:
2n-12-n<n-n; n-12<0.

Add 12 to both sides:
n-12+12<0+12; n<12.

This means there were less than 12 boxes. The next number down is 11; this woks because Mark sold 10 less than n; 11-10=1. Mark sold at least 1 box.

If n=10, however, 10-10=0; this doesn't work, because Mark did sell at least 1 box.