Answer:
The amount of time after which he will be earning $10.00 per hour is 11.9 years.
Explanation:
Given : Suppose that a new employee starts working at $7.03 per hour and receives a 3% raise each year. After time t, in years, his hourly wage is given by the equation
 .
.
To find : The amount of time after which he will be earning $10.00 per hour ?
Solution :
The equation is
 .
.
The amount of time after which he will be earning $10.00 per hour.
i.e. y=$10
Substitute in the equation and solve,
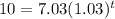
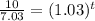
Taking log both side,
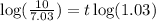
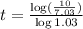
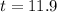
Therefore, the amount of time after which he will be earning $10.00 per hour is 11.9 years.