Question

when two fractions refer to the same whole and have the same denominators, explain why you can compare only the numerators

Answer 1

Because the denominator of the whole is exactly the same denominator of the fractions.

Explanation:

Let:

`a, b,c,d,e,f,K`

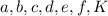
Arbitrary constants, where:

`K=(e)/(f)`

`\{a, b,c,d,e,f,K\} \in Z`

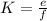
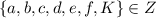
Let's rewrite the problem this way:

`K=(a)/(b) \pm (c)/(d)`

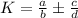
Where:

`(a)/(b) \pm (c)/(d)=(ad\pm bc)/(bd)`

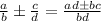
If the fractions have the same denominator, that is:

`b=d`

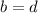
Then:

`(a)/(b) \pm (c)/(d)=(ad\pm bc)/(bd)=(ad\pm dc)/(d^2)`

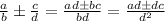
Factor:

`(d(a\pm c))/(d(d)) =(a\pm c)/(d)`

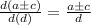
Thus:

`K=(e)/(f) = (a\pm c)/(d)`

As you can see from the equation, you can conclude directly from it that:

`f=d`

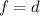
In another words, when two fractions refer to the same whole and have the same denominators, the denominator of the whole is exactly the same denominator of the fractions. That's the reason why you can compare only the numerators.

Answer 2

When two fractions with the same denominators are used to refer the same whole numbers have have the same denominator, you compare only the numerator because the denominators are already equal and the only sufficient part to confirm that the fractions are equal is if the denominators are equal. This is because the only way two fractions with the same denominator can be equal to each other is if they both have equal numerators.