Question

Are the two triangles below similar?

A) Yes; they have proportional corresponding sides
B) No; they do not have proportional corresponding sides
C)Yes; they have congruent corresponding angles
D) No; they do not have congruent corresponding angles

Answer 1

C)Yes; they have congruent corresponding angles

Answer 2

Option C

Yes, they have congruent corresponding angles.

Step-by-step explanation:

In ΔMNO

Given:
`\angle MNO = 105^(\circ)` ,
`\angle NMO = 48^(\circ)`

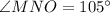The sum of measures of these three angles of triangle MNO is 180 degree.

Then;

`\angle MNO + \angle NMO + \angle MON= 180^(\circ)`

`105^(\circ)+ 48^(\circ) + \angle MON= 180^(\circ)`

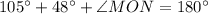
or

`153^(\circ) + \angle MON= 180^(\circ)`

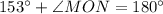
Simplify:

`\angle MON= 180^(\circ)-153^(\circ)= 27^(\circ)`

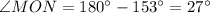
Similarly,

In a given triangle PQR; find angle QPR

`\angle PQR + \angle PRQ + \angle QPR= 180^(\circ)`

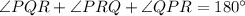
Substitute the value of angles PQR , angle PRQ from the given figure in above equation, we have

`105^(\circ)+ 27^(\circ) + \angle QPR= 180^(\circ)`

or

`132^(\circ) + \angle QPR= 180^(\circ)`

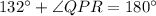
Simplify:

`\angle QPR= 180^(\circ)-132^(\circ)= 48^(\circ)`

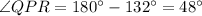
Then;

In ΔMNO and ΔPQR

`\angle MNO =\angle PQR = 105^(\circ)`

`\angle NMO =\angle QPR = 48^(\circ)`

`\angle MON =\angle PRQ= 27^(\circ)`

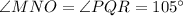
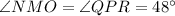
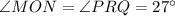
If all pairs of corresponding angles in a pair of triangles are congruent, then the triangles are Similar.

Therefore, ΔMNO
`\sim`ΔPQR .