
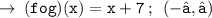
____________________________________
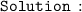

and
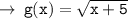
Now,
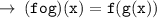
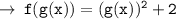
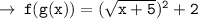


And here, x can have any real value. because there's no condition where " x + 7 " is not defined and neither it is in indeterminate form.
Therefore, it's domain is All Real. i.e (-∞ , ∞)
Answered by : ❝ AǫᴜᴀWɪᴢ ❞