Question

Express the limit as a definite integral on the given interval. lim n→∞ n xi ln(2 + xi2) δx, [0, 3] i = 1

Answer 1

`\displaystyle\lim_(n\to\infty)\sum_(i=1)^n x_i \ln(2+{x_i}^2)\,\Delta x=\int_0^3x\ln(2+x^2)\,\mathrm dx`

Answer 2

The given expression is:

`\lim_(n \to \infty) \sum x_(i)ln(2x+x_(i) ^(2)) \Delta x`

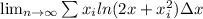
This expressions represent the sum of certain numbers of rectangles that comprehend the area under a curve, where the number of rectangles tend to infinite. Actually, this definition states that when
`n` tend to infinite, there's the area under the curve.

However, this can be expresses as a definite integral, which tend to have more sense for students:

`\int\limits^3_0 {xln(2+x^(2))} \, dx`

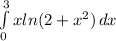
With the integral form can be shown better what we tried to say before. The integral represents the area under the given function
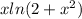`xln(2+x^(2))`, but just the part inside the interval from 0 to 3. The limit also refers to this, but in a different notation.