Let
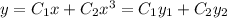
. Then
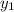
and
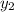
are two fundamental, linearly independent solution that satisfy
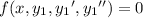
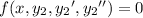
Note that
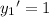
, so that

. Adding
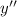
doesn't change this, since
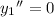
.
So if we suppose
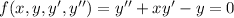
then substituting
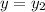
would give
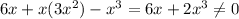
To make sure everything cancels out, multiply the second degree term by
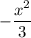
, so that
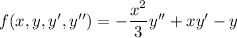
Then if
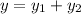
, we get
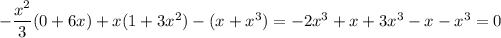
as desired. So one possible ODE would be

(See "Euler-Cauchy equation" for more info)