Question

I really need help with this, lol: Using the table of values given, determine the equation of the function that would model this data:

Answer 1

Somewhat optimistically, we guess that this function is a polynomial, since it doesn't immediately look like it follows an exponential or logarithmic pattern.

We can solve for the equation of degree
`n` passing through
`n` points by writing the polynomial in the form:


`c_n x^n + c_(n-1) x^(n-1) + \cdots + c_0 = f(x)`.

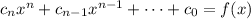
Then, we solve for the values of the sequence
`c` by substituting in
`n` pairs
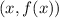
`(x, f(x))`. This gives us the polynomial of degree
`n` satisfying the conditions for the first
`n` points; afterwards, we have to check if this polynomial works for the other points. If it does, it is the solution, otherwise, we need to keep going.

Testing in this manner, degrees zero, one, and two don't work. When we try degree three, however, we get the system of equations:


`c_3+c_2+c_1+c_0=0`

`8c_3+4c_2+2c_1+c_0=3`

`27c_3+9c_2+3c_1+c_0=16`

`64c_3+16c_2+4c_1+c_0=45`

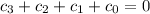
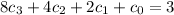
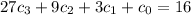
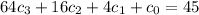
Solving this system gives
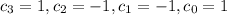
`c_3 = 1, c_2 = -1, c_1 = -1, c_0 = 1`. Substituting
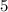
`5` into this polynomial,
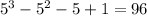
`5^3-5^2-5+1=96`. Likewise,
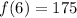
`f(6) = 175`, so this polynomial satisfies all of the conditions listed.

We therefore conclude that
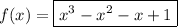
`f(x) = \boxed{x^3-x^2-x+1}`.