Question

The equation 2x2 – 5x = –12 is rewritten in the form of 2(x – p)2 + q = 0. what is the value of q?

Answer 1

2x^2 - 5x + 12 = 0
Factoring out the leading coefficient:
2(x^2 - 5/2 x) + 12 = 0
Completing the square:
2[(x - 5/4)^2 - 25/16] + 12 = 0
2(x - 5/4)^2 - 25/8 + 12 = 0
2(x - 5/4)^2 + 71/8 = 0
q = 71/8

Answer 2

`q=(71)/(8)`

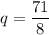
Explanation:

The given equation is

`2x^2-5x=-12`

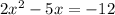
Rewrite the given equation in the form of

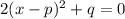`2(x-p)^2+q=0` ... (i)

We need to find the value of q.

The given equation can be rewritten as

`2(x^2-(5)/(2)x)=-12`

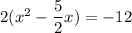
Now, add and subtract square of half of coefficient of x inside the parenthesis.

`2(x^2-(5)/(2)x+((5)/(4))^2-((5)/(4))^2)=-12`

`2(x^2-(5)/(2)x+((5)/(4))^2)-2((5)/(4))^2)=-12`

`2(x-(5)/(4))^2-2((25)/(16))=-12`

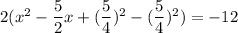
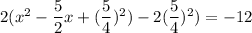
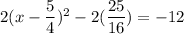
Add 12 on both sides.

`2(x-(5)/(4))^2-(25)/(8)+12=0`

`2(x-(5)/(4))^2+(96-25)/(8)=0`

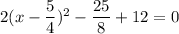
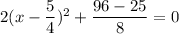
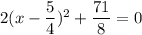`2(x-(5)/(4))^2+(71)/(8)=0` ... (ii)

From (i) and (ii), we get

`q=(71)/(8)`

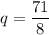
Therefore,
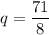`q=(71)/(8)`.