Question

What is the sum of the arithmetic series of odd numbers below?1 + 3 + 5 + ... + 25?

Answer 1

Given from question
a = 1
an = 25
b = a₂ - a = 3 - 1 = 2

Asked from question
Sn

Solution
The general formula for finding the sum of arithmetic series is
Sn = n/2 (a + an)

Because we don't know yet the value of n, we should find it first, with this,
an = a + d(n - 1)
25 = 1 + 2(n - 1)
25 = 1 + 2n - 2
25 = 2n - 1
2n = 24
n = 12

After finding the value of x, calculate the sum of series by the formula I mentioned above
Sn = n/2 (a + an)
S₁₂ = 12/2 (1 + 25)
S₁₂ = 6 (26)
S₁₂ = 156

The sum of the series is 156

Answer 2

Sum of the arithmetic series of odd numbers 1 + 3 + 5 + ... + 25 is 169 .

Explanation:

Formula of airthmetic series

`a_(n)=a_(1)+(n-1)d`

`S_(n) = (n(a_(1)+a_(n)))/(2)`

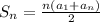
Where n is the nth term ,
`a_(n)` is the nth term , d is the common difference and
`a_(1)` is the first term .

As the airthmetic series given in the question .

1 + 3 + 5 + ... + 25

`a_(1)= 1`

`a_(2)= 3`

`d=a_(2)-a_(1)`

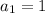
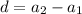
d = 3 - 1

d = 2

`a_(n)= 25`

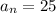
Put all the values in the formula

`25=1+(n-1)2`

25 - 1 = 2n - 2

24 + 2 = 2n

26 = 2n

`n = (26)/(2)`

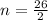
n = 13

Now put the values in the another formula

`S_(n) = (13* (1+25))/(2)`

`S_(n) = (13* (26))/(2)`

`S_(n) = 13* 13`

`S_(n) = 169`

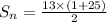
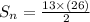
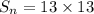
Therefore the sum of the arithmetic series of odd numbers 1 + 3 + 5 + ... + 25 is 169 .