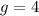Question

Solve the system of equations using the linear combination method

6g+8h=40
-6g+2h=-20
Enter your answer in the boxes
G=
H=

Answer 1

The solution to the given system of equations is
g = 4
h = 2

Answer 2

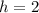`h=2` and
`g=4`

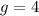
Explanation:

In the combination method, both equations are added or subtracted so that a variable is eliminated and it is possible to determine the value of the remaining variable.

We have the equations:

`6g+8h=40`

`-6g+2h=-20`

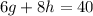
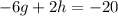
In this case, if we add the two equations given, g will be eliminated and we could find the value of h.

• Adding the equations:

`6g+8h=40\\+(-6g+2h=-20)`

----------------------------------

`6g+(-6g)+8h+(+2h)=40+(-20)\\=6g-6g+8h+2h=40-20\\0g+10h=20\\10h=20\\h=(20)/(10) =2`

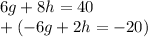
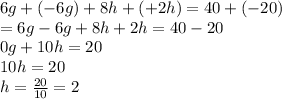
We have
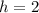`h=2`, Now we only need
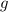`g`, so we substitute the value of
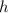`h` in any of the original equations:

`6g+8h=40`

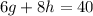
since
`h=2`

`6g+8(2)=40`

`6g+16=40`

`6g=40-16`

`6g=24`

`g=(24)/(6) =4`

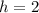
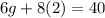
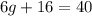
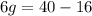
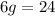
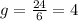
so the answer is
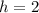`h=2` and
`g=4`