QUESTION 1
The given system of equation is
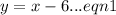
and
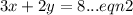
Let us substitute equation (1) into equation (2) to get,
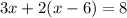
We expand the bracket to get,
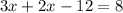
We simplify to get.
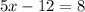
We group like terms to get
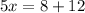
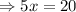
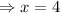
We now substitute
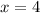 in to equation (1) to obtain,
in to equation (1) to obtain,
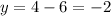
The correct answer is option A.
QUESTION 2
The given system of equations is
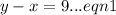
and
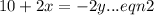
We make y the subject in equation (2) to get,
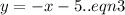
We put equation (3) into equation (1) to obtain,
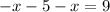
We group like terms to get,
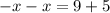
This implies that,
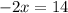
We divide through by
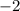 to get,
to get,
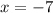
Hence the x-coordinate is
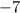
QUESTION 3
The given system is
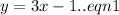
and
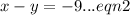
We make
 the subject in equation (2) to get,
the subject in equation (2) to get,
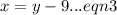
We put equation (3) into equation (1) to obtain,
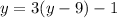
We expand the bracket to get,
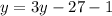
Group like terms to get,
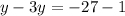
We simplify to get;
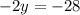
This implies that,
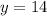
Therefore the y-coordinate is 14.