Question

Answers fast please. 1.) y=x−63x+2y=8 Use the substitution method. A.) (4, −2) B.) (14, 8) C.) (0, −6) D.) (3, −3) 2.) What is the x-coordinate of the solution for the system of equations? {y−x=910+2x=−2y X= what? 3.) What is the y-coordinate of the solution for the system of equations? {y=3x−1x−y=−9 Y=what?

Answer 1

1.
A.) (4, −2)

2.
x = -7
y = 2

3.
x = 5
y = 14

Answer 2

QUESTION 1

The given system of equation is

`y=x-6...eqn1`

and

`3x+2y=8...eqn2`

Let us substitute equation (1) into equation (2) to get,

`3x+2(x-6)=8`

We expand the bracket to get,

`3x+2x-12=8`

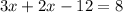
We simplify to get.

`5x-12=8`

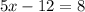
We group like terms to get

`5x=8+12`

`\Rightarrow 5x=20`

`\Rightarrow x=4`

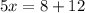
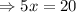
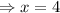
We now substitute
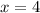`x=4` in to equation (1) to obtain,

`y=4-6=-2`

The correct answer is option A.

QUESTION 2

The given system of equations is

`y-x=9...eqn1`

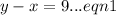
and

`10+2x=-2y...eqn2`

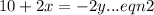
We make y the subject in equation (2) to get,

`y=-x-5..eqn3`

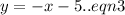
We put equation (3) into equation (1) to obtain,

`-x-5-x=9`

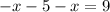
We group like terms to get,

`-x-x=9+5`

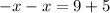
This implies that,

`-2x=14`

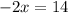
We divide through by
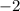`-2` to get,

`x=-7`

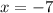
Hence the x-coordinate is
`-7`

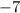
QUESTION 3

The given system is

`y=3x-1..eqn1`

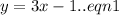
and

`x-y=-9...eqn2`

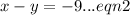
We make
`x` the subject in equation (2) to get,

`x=y-9...eqn3`

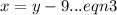
We put equation (3) into equation (1) to obtain,

`y=3(y-9)-1`

We expand the bracket to get,

`y=3y-27-1`

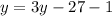
Group like terms to get,

`y-3y=-27-1`

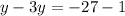
We simplify to get;

`-2y=-28`

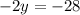
This implies that,

`y=14`

Therefore the y-coordinate is 14.