Answer:

Explanation:
The initial point of the vector is at (7,-9).
The terminal point of the vector is at (-17,4).
First, we need to find the same vector with initial point at the origin of the coordinate system. We do that by finding its horizontal length and its vertical length.
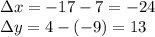
So, the vector with initial point at the origin is
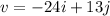
Where
 represents horizontal direction and
represents horizontal direction and
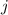 represents vertical direction.
represents vertical direction.
Now, we need to find the module of this vector
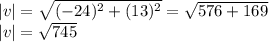
The uni vector is defined by the quotient between the vector and its module.

Replacing each part, we have
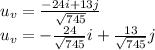
Therefore, the right answer is the third choice.