Question

Find two consecutive even whole numbers whose product is 288

Answer 1

Let's write an equation describing the problem.

Any even whole number may be represented by writing
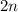
`2n` in which
`n` is any non-negative integer.

It follows that for a even whole number
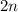
`2n` the next (consecutive) even whole number can be written as
`2(n+1)`.

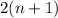
We now need to solve the following equation:


`2n*2(n+1)=288`

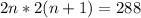
If we solve for
`n` we get:


`n=-9 ,8`

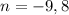
We have to values, as the equation is quadratic. We take the positive one as the correct one. So
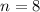
`n=8`, and if we plug in this value to
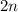
`2n` and
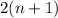
`2(n+1)` we know that the asnwer is 16 and 18.