Question

What are the explicit equation and domain for a geometric sequence with a first term of 4 and a second term of −12? an = 4(−3)n − 1; all integers where n ≥ 1 an = 4(−3)n − 1; all integers where n ≥ 0 an = 4(36)n − 1; all integers where n ≥ 1 an = 4(36)n − 1; all integers where n ≥ 0

Answer 1

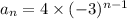`a_(n) = 4 * (-3)^(n-1)`; all integers where n ≥ 1

Explanation:

We are given that the first term of the sequence is 4 i.e.
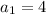`a_(1) =4` and second term is -12 i.e.
`a_(2) = -12`.

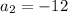Now, the nth term of geometric sequence is given by,

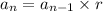`a_(n) = a_(n-1) * r`, where r is the common ratio of the sequence.

So, using the given values we get,

`a_(2) = a_(1) * r`

i.e.
`r = (a_(2) )/(a_(1) )`

i.e.
`r = (-12)/(4)`

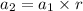
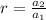
i.e. r = -3.

Now the explicit formula for the geometric equation is given by,

`a_(n) = a_(1) * r^(n-1)`.

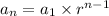i.e.
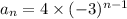`a_(n) = 4 *(-3)^(n-1)`, where
`n\geq 1`

Hence option first is correct.

Answer 2

The geometric sequence is given by:
an=ar^(n-1)
where:
a=first term
r=common ratio
n is the nth term
given that a=4, and second term is -12, then
r=-12/4=-3
hence the formula for this case will be:
an=4(-3)^(n-1)
where n≥1