Answer:
g = 3
Step-by-step explanation:
Given: Expression
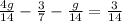
We have to solve for g .
Consider the given expression
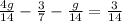
Cancel common factor 2,
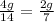
Expression becomes,

Multiply both side by LCM = 14

Simplify, we have,
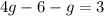
Adding g both side , we have,
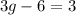
Adding 6 both side, we have,
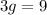
Divide both sde by 3, we have,
g = 3
Thus, g = 3