Question

opal deposited 2925.90$ into a savings account with an interest rate of 3.9% compounded twice a year. about how long will it take for the account to be worth 6000$

Answer 1

Use the compound amount formula:

A = P (1 + r/n)^( r/n )

Here,

A $6000 = $2925.90 ( 1 + 0.039/2 )^(2t). We must solve for t.

2.051 = ( 1 + 0.0195 )^(2t)

Take the natural log of both sides:

ln 2.051 = (2t) ln 1.0195 leads to (2t) ( 0.0193 ) = 0.7183

0.7183
Then 2t = -------------- = 37.219
0.0193
37.219
Finally, t = ------------- = 18.6 years
2

This is reasonable, because we're going from $2925.90 to more than twice that, or $6000, at the relatively low interest rate of 3.9%.

Answer 2

It will take 18.55 years.

Explanation:

The formula of Compound Interest is:

`A = P(1+(r)/(n))^(nt)`

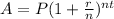
where A = Amount

P = Principle

r = rate

n = Number of Compounding per year

t = total number of year

Here, P = 2925.9, r = 3.9% = 0.039, n = 2, A = 6000, and t = ?.

Putting all these values in above formula:

`6000 = 2925.9(1+(0.039)/(2))^(2* t)`

⇒
`6000 = 2925.9((2.039)/(2))^(2t)`

⇒
`6000 = 2925.9(1.0195)^(2t)`

⇒
`6000 ÷ 2925.9 = (1.0195)^(2t)`

⇒
`2.05 = (1.0195)^(2t)`

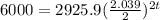
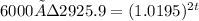
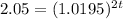
Taking log on both side

log(2.05) = 2t × log(1.0195)

⇒ 0.3117 = t × 0.0167

⇒ t = 18.55

Hence, Opal will get $6000 after 18.55 years.