Answer:
Inverse function is
![f^(-1)=\sqrt[3]{(1)/(x)}](https://img.qammunity.org/2019/formulas/mathematics/high-school/naoab4zhn85avu91o7inkr5sa5kx9r9xaq.png)
It is a function
Explanation:
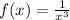
Replace f(x) with y
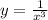
Now we replace x with y and y with x
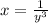
Now multiply by y^2 on both sides and solve for y
xy^3 = 1
divide by x on both sides
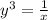
Take cube root on both sides
![y=\sqrt[3]{(1)/(x) }](https://img.qammunity.org/2019/formulas/mathematics/high-school/q44by1whdi4j190fay8icjcbkqoozqh4q5.png)
Inverse function is
![f^(-1)=\sqrt[3]{(1)/(x)}](https://img.qammunity.org/2019/formulas/mathematics/high-school/naoab4zhn85avu91o7inkr5sa5kx9r9xaq.png)
For every value of x there is a y value . for each input there is only one output
so it is a function