Question

A student is attempting to convert a slope-intercept equation into standard form. Which of the following statements best applies to the sample math given below?

Given y=1/4x+2, I first isolate the constant. After doing so, I get the equation -1/4x+y=2. To remove the fraction, I multiply by –4, giving the equation x-4y=2, which is the final answer.


A.
the work shown to isolate the constant is not correct
B.
the work shown to remove all fractions is not correct
C.
the final answer is not in standard form
D.
the work shown is correct

Answer 1

the answer is B. They did not multiply the constant 2 by 4 when multiplying through to remove the fraction. so the correct answer would be x-4y=-8

Answer 2

The work shown to remove all fractions is not correct

Explanation:

Given Work:

`y=(1)/(4)x+2`

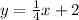
I first isolate the constant.

After doing so, I get the equation
`-(1)/(4)x+y=2`

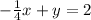
To remove the fraction, I multiply by –4, giving the equation x-4y=2, which is the final answer.

Correct Work:

`y=(1)/(4)x+2`

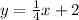
First isolate the constant.

So, obtained equation :
`y-(1)/(4)x=2`

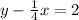
To remove the fraction, Multiply the obtained equation by –4

So, Equation :
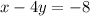`x-4y=-8` Which is the final answer

On comparing both the work we can see that in the given work the removal of fraction is done incorrectly

They didn't multiply -4 on the right hand side .

So, Option B is correct

The work shown to remove all fractions is not correct