Question

What is the value of x? Enter your answer in the box. x = A triangle with midsegment parallel to the base. the left side is labeled 40 c m below the midsegment and 5 c m above the midsegment. the right side is labeled 2 x + 10 c m below the midsegment and 3 c m above the midsegment.

Answer 1

the value of x is 7 cm

Explanation:

Answer 2

Answer: The value of x is 7 cm.

Explanation:

Let ABC is a triangle with mid -segment DE parallel to the base BC.

the left side is labeled 40 cm below the mid -segment

i.e. BD = 40 cm

the left side is labeled 5 cm above the mid -segment

i.e. AD = 5 cm

Similarly,

The right side is labeled 2 x + 10 cm below the mid -segment

i.e. EC = 2x+10

The right side is labeled 3 cm above the mid -segment

i.e. AE = 3 cm

So, By Basic proportionality theorem,

The ratio of the other two sides is equal.

`(AD)/(DB)=(AE)/(EC)\\\\(5)/(40)=(3)/(2x+10)\\\\(1)/(8)=(3)/(2x+10)\\\\2x+10=24\\\\2x=24-10\\\\2x=14\\\\x=(14)/(2)\\\\x=7 cm`

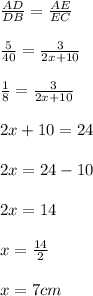
Hence, the value of x is 7 cm.