Question

The area of a rectangle is 108m2 and its diagonal is 15m. Find the perimeter of the rectangle if the sides are of integer lengths.

Answer 1

Considering the figure,

In ΔABC, right angled at B, we can use Pythagoras theorem :

`x^2 + y^2 = 15^2`

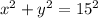
`x^2 + y^2 = 225`..................(1)

Also we are given area of rectangle as 108 m²

Area of rectangle = length * breadth = x * y

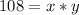`108 =x*y`.............(2)

`x=108/y`........(3)

plugging the value of x from equation (3) in (1),

`x^2 + y^2 = 225`

`(108/y)^2 + y^2 = 225`

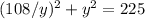
We can use quadratic formula to solve this.

On solving this we get four values of y as :

y=12, y=-12, y=9 and y=-9

since length cannot be negative we have two y values as :

y=12 and y=9

plugging these in equation (3) to get x as

x=108/y = 108/12 = 9

x = 108/9 =12

so we have two answers:

length =9 m and breadth = 12m

length =12 m and breadth =9m

Perimeter = 2(l+b)

Perimeter = 2(9+12) = 42m