Question

4. The mass of ball A is 10 kilograms and the mass of ball B is 5 kilograms. If

the initial velocity is set to 3 meters per second for each ball, what is the
final velocity of ball B if the final velocity of ball A is 2 meters per second?
Use the elastic collision equation to find the final velocity of ball B. Assume
ball A initially moves from right to left and ball B moves in the opposite
direction. Identify each mass, velocity, and unknown. Show your work,
including units, and indicate the direction of ball B in your answer.

5. . If the mass of each ball were the same, but the velocity of ball A were twice
as much as ball B, what do you think would happen to the final velocity of
each ball after the collision? To answer this question, create a hypothesis in
the form of an if-then statement. The “if” is the independent variable, or the
thing that is being changed. The “then” is the dependent variable, or what
you will measure as the outcome.


Please help me! Thank you so much!

Answer 1

(4) It is given that :

Mass of ball A,
`m_A=10\ kg`

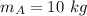
Mass of ball B,
`m_B=5\ kg`

Initial velocity of ball A,
`u_A=-3\ m/s`

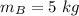
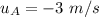
Initial velocity of ball B,
`u_B=3\ m/s`

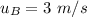
Final velocity of ball A,
`v_A=2m/s`

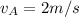
We have to find the final velocity of ball B after collision.

Since, it is a elastic collision. So the momentum remains conserved.

i.e.

`m_Au_A+m_Bu_B=m_Av_A+m_Bv_B`

`10\ kg* (-3\ m/s)+5\ kg*3\ m/s=10\ kg* 2\ m/s+5\ kg*v_B`

`-30+15-20=5v_B`

`-35\ m/s=5v_B`

`-7\ m/s=v_B`

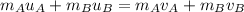
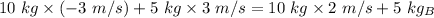
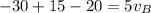
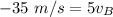
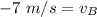
So, after collision the ball B moves from right to left with a speed of 7 m/s.

(5) In this part, the mass of each ball is same and velocity of ball A is twice of that of ball B such that

`u_A=2u_B`

`m_A=m_B=m`

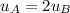
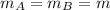
If the collision of two balls is elastic, then using the conservation of momentum as

`3u_B=v_A+v_B`

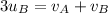
This implies that the final velocities would be different.

If the collision is inelastic,

`3v_b=2mv_f`

`v_f=(3v_b)/(2)`

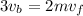
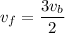
So, if there is inelastic collision the balls will move with a common velocities.

Answer 2

4.) We are told that ball A is travelling from right to left, which we will refer to as a positive direction, making the initial velocity of ball A, +3 m/s. If ball B is travelling in the opposite direction to A, it will be travelling at -3 m/s. The final velocity of A is +2 m/s. Using the elastic collision equation, which uses the conservation of linear momentum, we can solve for the final velocity of B.

MaVai + MbVbi = MaVaf + MbVbf

Ma = 10 kg and Mb = 5 kg are the masses of balls A and B.
Vai = +3 m/s and Vbi = -3 m/s are the initial velocities.
Vaf = +2 m/s and Vbf = ? are the final velocities.

(10)(3) + (5)(-3) = (10)(2) + 5Vbf
30 - 15 = 20 + 5Vbf
15 = 20 + 5Vbf
-5 = 5 Vbf
Vbf = -1 m/s

The final velocity of ball B is -1 m/s.

5.) We are now told that Ma = Mb, but Vai = 2Vbi

We can use another formula to look at this mathematically.

Vaf = [(Ma - Mb)/(Ma + Mb)]Vai + [(2Mb/(Ma + Mb)]Vbi

Since Ma = Mb we can simplify this formula.

Vaf = [(0)/2Ma]Vai + [2Ma/2Ma]Vbi
Vaf = Vbi

Vbf = [(2Ma/(Ma + Mb)]Vai + [(Ma - Mb)/(Ma + Mb)]Vbi
Vbf = [2Mb/2Mb]Vai + [(0)/2Mb]Vbi
Vbf = Vai

Vaf = Vbi
Vbf = 2Vbi

If the initial velocity of A is twice the initial velocity of B, then the final velocity of A will be equal to the initial velocity of B.

If the initial velocity of A is twice the initial velocity of B, then the final velocity of B will be twice the initial velocity of B.