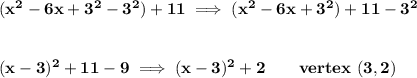Question

What is the vertex form of

`{x}^(2) - 6x + 11`
and how did you get the answer?

Answer 1

`\bf ~~~~~~\textit{parabola vertex form} \\\\ \begin{array}{llll} y=a(x- h)^2+ k\\\\ x=a(y- k)^2+ h \end{array} \qquad\qquad vertex~~(\stackrel{}{ h},\stackrel{}{ k})`

so, x²-6x + 11, let's do some grouping first

( x² - 6x ) +11

( x² - 6x + b² ) +11

now, what's our mystery fellow "b"? well, let's recall that the middle term in a perfect square trinomial is, (a - b)² = a² - 2ab + b², so the middle term is namely just 2 times the other two fellows, without the exponent.

now, here is 6x, so then
`\bf 2\cdot x\cdot b=6x\implies b=\cfrac{6x}{2x}\implies b=3`

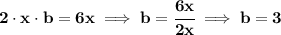
that means, that our fellow is 3 then, so we'll add 3², however, let's keep in mind that, all we're doing is, borrowing from our very good friend Mr Zero, 0.

so if we add 3², we have to also subtract 3², therefore,


`\bf (x^2-6x+3^2-3^2)+11\implies (x^2-6x+3^2)+11-3^2 \\\\\\ (x-3)^2+11-9\implies (x-3)^2+2\qquad vertex~(3,2)`