Answer :
Step 1 :
![A+B\rightleftharpoons AB(fast)\\Rate=K[A][B]](https://img.qammunity.org/2019/formulas/chemistry/college/tdvb5fivpmsnhd551xbudddwgot4qmblxl.png)
Step 2 :
![AB+B\rightarrow AB_2(slow)\\Rate=K[AB][B]](https://img.qammunity.org/2019/formulas/chemistry/college/ci6ff7rrzd5qns6z5ef2bdxvm4ryu5ubj5.png)
Step 3 :
![AB_2+B\rightleftharpoons AB_3(fast)\\Rate=K[AB_2][B]](https://img.qammunity.org/2019/formulas/chemistry/college/rabcrryuiqr3mscrw6gxbf36t8p37zcpdz.png)
overall reaction rate :
![Rate=K[A][B]^2](https://img.qammunity.org/2019/formulas/chemistry/college/s1kfabdmimybmpc2lb5eagqtw3vkqqauhj.png)
As we know that the slow step is the rate determining step of the chemical reaction that determines the rate at which overall reaction proceeds. But in the slow step reaction, intermediate AB is involved. As, the intermediate will get completely consumed in the reaction. Hence, the rate law for the overall equation is not the same as the rate equation for the rate-determining step.
To determining the overall reaction rate following steps are involved :
From the step 2, the rate is,
![Rate=K[AB][B]](https://img.qammunity.org/2019/formulas/chemistry/college/uk0e3jgiy7vzikm2p16ov3yx6szq1lx279.png) ...........(A)
...........(A)
Now we have to determine the equilibrium expression from the step 1 reaction.
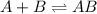
![K=([AB])/([A][B])](https://img.qammunity.org/2019/formulas/chemistry/college/ae8h4hon1jaatlteacw80xvr8p2e6x5ce2.png)
![[AB]=K[A][B]](https://img.qammunity.org/2019/formulas/chemistry/college/bwjb2m5jdn8nuv0g3p9f1yzilb1pbcj509.png)
Now put the value of [AB] in equation (A), we get
![Rate=KK[A][B][B]](https://img.qammunity.org/2019/formulas/chemistry/college/cav6f95z5j29sgm06myb92mfag17y9ruz8.png)
KK become new constant K'
![Rate=K'[A][B]^2](https://img.qammunity.org/2019/formulas/chemistry/college/331b7m36rt74b4vewhu1hnnynpgu5a0hs7.png)
Thus, this is the overall rate of reaction.