Question

What is the range for f(x)=x^6+kx^4-9x^2-27?

Answer 1

Substitute
`y` for
`x^2` to find that this function is equivalent to:


`y^3 + ky^2 - 9y - 27`

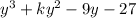
We take the derivative with respect to
`y` to find the local minima, which occur at the solutions to:


`3y^2 + 2ky - 9 = 0`

Using the quadratic formula gives:


`y = (-2k \pm √(4k^2 + 108))/(6)`

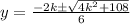
By the Trivial Inequality, since
`y=x^2`,
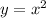
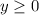
`y \geq 0`, so
`y=(-2k + √(4k^2 + 108))/(6) = (-k + √(k^2 + 27))/(3)`.

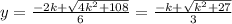
To determine whether this is a local minimum or a local maximum, we compute the second derivative, which is
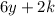
`6y+2k`. This is positive for all positive values of
`k` (a reasonable assumption, since things get really messy really quickly otherwise), so the function is concave up at these values. Hence, this value is a local minimum.

Since it is the only local minimum, we conclude that it is the global minimum, since as
`x` goes to positive or negative infinity, the
`x^6` term dominates and makes the function become extremely large.

The arithmetic gets pretty messy from here (I used WolframAlpha to ensure that I didn't make any mistakes), but in short, the rest of the problem pretty much devolves to substituting this value for
`y` back in, which gives you
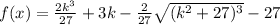
`f(x) = (2k^3)/(27) + 3k - (2)/(27) √((k^2 + 27)^3) - 27` as the minimum.

Now, to show that there is no maximum, note that
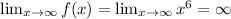
`\lim_(x \to \infty) f(x) = \lim_(x \to \infty) x^6 = \infty`. Hence, the range of
`f(x)` is
`[(2k^3)/(27) + 3k - (2)/(27) √((k^2 + 27)^3) - 27, \infty)`.