First list all the positive and negative factors of the constant term in the expression: ±(1,2,3,4,6,12) these will be the values for "p"
Second list all the positive and negative factors of the leading coefficient:
±(1,3) these will be the values for "q"
Now list all the possible values of

these will be the possible rational zeros of the polynomial function:
±(
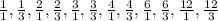
)
these can be reduced to the following list:
±(1,
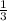
, 2,
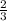
, 3, 4,
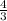
, 6, 12
This list represents the possible rational zeros of the function. You can then use synthetic division to narrow down the actual roots of the function.