The answer is: "
41 .12"
units² .
_______________________________________________________Step-by-step explanation:_______________________________________________________The combined area = the area of a semi-circle (half-circle); PLUS the area of the triangle.
_______________________________________________________The area, "A", of a triangle:
A = (b * h) / 2 ; in which b = base; and "h = perpendicular height" ;
From the diagram: "b = 8" ; "h = distance from "(4, 1)" to "(4, 5)" = 4 ;
A = (b * h) / 2 = (8 * 4) / 2 = 32/2 = 16 units²
_______________________________________________________The area of the "half of a circle" :
Note: The area, "A" ; of a [FULL] circle:
A =
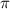
* r² ;
in which: r = radius = 4 ; {as shown in figure attached;
We are told to use the approximation of "3.14" for
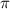
;
A = (3.14) * 4² = 3.14 * 16 ;
To get the area of "one-half" that circle; we divide this value by "2" ;
Area of "half-circle" =
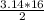
;
The "
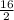
" result in "8" ;
And we know have: "3.14 * 8" ;
3.14 * 8 = 25.12 units²
_____________________________________________The total area of the figure =
16 units² + 25.12 units² =
_____________________________________________ 41 .12 units² .
_____________________________________________