Question

How to solve question 1a? very confused?

Answer 1

a)


`\bf y=x\left( 1-\cfrac{2}{x}+x \right)\implies y=x-2+x^2 \\\\\\ \cfrac{dy}{dx}=1-0+2x\implies \left. \cfrac{dy}{dx}=1+2x \right|_(x=1)\implies \stackrel{m}{3} \\\\\\ \stackrel{\textit{point-slope form}}{y- y_1= m(x- x_1)}\quad \begin{cases} x=1\\ y=0\\ m=3 \end{cases}\implies y-0=3(x-1) \\\\\\ y=3x-1`

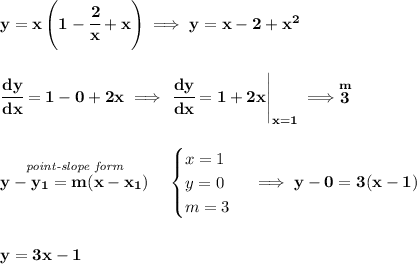
b)

recall that the is the equation of the tangent line at (1,0), whose slope is 3 of course, now, the normal will be the line that's perpendicular to the tangent line, and therefore it will have a slope that is negative reciprocal to the tangen't line's slope, thus


`\bf \textit{perpendicular, negative-reciprocal slope for slope}\quad 3\implies \cfrac{3}{1}\\\\ negative\implies -\cfrac{3}{ 1}\qquad reciprocal\implies - \cfrac{ 1}{3}\\\\ -------------------------------\\\\ \stackrel{\textit{point-slope form}}{y- y_1= m(x- x_1)}\quad \begin{cases} x=1\\ y=0\\ m=-(1)/(3) \end{cases}\implies y-0=-\cfrac{1}{3}(x-1) \\\\\\ y=-\cfrac{1}{3}x+\cfrac{1}{3}`

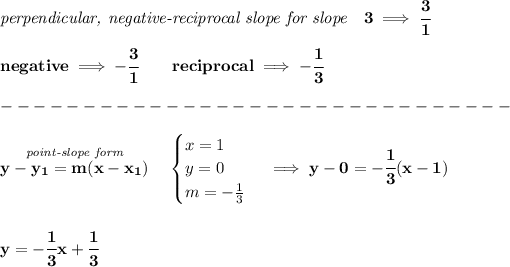
now, for the second bit there,


`\bf sin\left( √(x^2+1) \right)\implies sin\left[ ( x^2+1 )^{(1)/(2)} \right] \\\\\\ \stackrel{chain~rule}{cos\left[ ( x^2+1 )^{(1)/(2)} \right]\cdot \cfrac{1}{2}( x^2+1 )^{-(1)/(2)}\cdot 2x} \\\\\\ cos\left[ ( x^2+1 )^{(1)/(2)} \right]\cdot \cfrac{x}{( x^2+1 )^{(1)/(2)}}\implies \cfrac{x~cos\left( √(x^2+1)\right)}{√(x^2+1)}`