Answer:
a. 41√3 unit
b. 82 unit
Explanation:
Let ABC is a triangle,
In which m∠B = 90°,
m∠A= 30°, m∠C = 60°,
Also, BC = 41 feet,
a. By the law of sine,
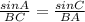
By substituting the value,
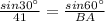
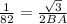
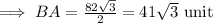
b. AC is the hypotenuse of the triangle ABC,
By the pythagoras theorem,
