Question

Emma earns $6 each time she mows the lawn and $8 per hour for babysitting. She is saving up to buy a new pair of jeans that cost $48. If she mows the lawn x times and babysits for y hours, which graph shows the amount of work she needs to complete to earn at least enough to purchase the new jeans?

Answer 1

The graph in the attached figure

Explanation:

Let

x------> the number of times Emma mows the lawn

y------> the number of hours Emma babysits

we know that

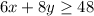`6x+8y\geq 48` ------> inequality that represent the situation

The solution is the shade area above the solid line between the values of x and y positive

The equation of the solid line is equal to
`6x+8y=48`

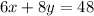
The slope of the line is negative
`m=-(3)/(4)`

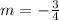
The y-intercept of the line is the point
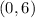`(0,6)` (value of y when the value of x is equal to zero)

The x-intercept of the line is the point
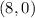`(8,0)` (value of x when the value of y is equal to zero)

so

The graph in the attached figure