Question

One of the x-intercepts of the parabola represented by the equation y = 3x^2 + 6x − 10 is approximately (1.08, 0).

The other x-intercept of the parabola is approximately ______.
(Round to the nearest hundredth)

Answer 1

3x^2 + 6x - 10 = 0

x = [-6 +/- sqrt(^2 - 3*3*-10)] / 2*3

= 1.08 and -3.08

Other x -intercept is (-3.08,0)

Answer 2

`(-3.08,0)`.

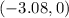Explanation:

We have been given that one of the x-intercepts of the parabola
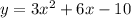`y=3x^2+6x-10` is approximately (1.08, 0). We are asked to find the another x-intercept of parabola.

We will use quadratic formula to solve our given problem.

`x=(-b\pm √(b^2-4ac))/(2a)`

Upon substituting our given values in above formula we will get,

`x=(-6\pm √(6^2-4*3*-10))/(2*3)`

`x=(-6\pm √(36+120))/(6)`

`x=(-6\pm √(156))/(6)`

`x=(-6+√(156))/(6)\text{ or }x=(-6-√(156))/(6)`

`x=-1+2.081665999466\text{ or }x=-1-2.081665999466`

`x=1.081665999466\text{ or }x=-3.081665999466`

`x\approx 1.08\text{ or }x\approx -3.08`

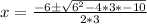
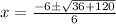
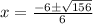
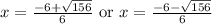
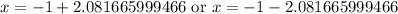
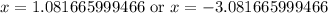
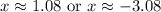
Therefore, the other x-intercept of the parabola is approximately
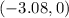`(-3.08,0)`.