Answer: The range is
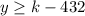
The way to get this answer isn't completely obvious. What I did first was graph the function using GeoGebra allowing k to be a parameter. With k as a sliding parameter, the graph was able to be slid up and down the screen. The basic shape of the curve is a distorted W shape. The lowest point being the local minimum. Which is where the lower endpoint of the range would be.
Using the derivative, we can get
y = x^4 + 8x^3 + k
dy/dx = 4x^3 + 24x^2
set dy/dx equal to zero and solve for x
dy/dx = 0
4x^3 + 24x^2 = 0
4x^2(x + 6) = 0
4x^2 = 0 or x+6 = 0
x = 0 or x = -6
It turns out that x = 0 is a saddle point so we can ignore this value. Only x = -6 is where the local min is at. Plug this back into the original function
y = x^4+8x^3+k
y = (-6)^4+8(-6)^3+k
y = -432+k
y = k - 432
So when the input is x = -6, the output is k - 432 for some value k
In other words, the smallest y can get is k - 432. Otherwise it will be larger than this value
So that's why the range is
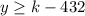
Note: if this calculus approach doesn't make much sense, then you can try various k values and use a calculator to find the lowest point. Making a table of k values with the corresponding lowest point would hopefully point you in the right direction.