Question

On an ice rink, two skaters of equal mass grab hands and spin in a mutual circle once every 2.3 s . if we assume their arms are each 0.85 m long and their individual masses are 65.0 kg , how hard are they pulling on one another

Answer 1

We have to
m = 65 kg
r = 0.85 m
t = 2.3 s
The perimeter of the circle is given by:
P = 2 * pi * r
P = 2 * pi * (0.85 m)
P = 5.34 m
Then, by definition, the distance equals the speed by time:
d = v * t
v = d / t
v = (5.34 m) / (2.3 s)
v = 2.32 m / s
Then, to find the radial acceleration, we must use the speed found and the radius of the circle:
a = v ^ 2 / r
a = (2.32 m / s) ^ 2 / (0.85 m)
a = (5.38 m ^ 2 / s ^ 2) / (0.85 m)
a = 6.32 m / s ^ 2
Finally, we have that by definition the force is equal to the mass by acceleration:
F = m * a
F = (65 kg) * (6.32 m / s ^ 2)
F = 410.8 N
answer
F = 410.8 N

Answer 2

Time taken to complete on complete circle = 2.3 seconds

Radius of circle (r) = 0.85 (length of each arm)

Speed of skaters =
`(Distance)/(time)`

`Speed = (2\pi r)/(t)`

`Speed = (2 * 3.14 * 0.85)/(2.3)`

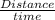
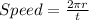
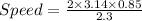
Speed (v) = 2.32 m/s

Let the force applied by one skater on the other be F

F(net) = centripetal force

`F = (mv^2)/(r)`

`F = (65 * 2.32^2)/(0.85)`

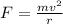
F = 411.59 Newtons

Hence, the force applied by each skater on the other is: F = 411.59 Newtons